The Binomial Standard Deviation Calculator computes the standard deviation of a binomial distribution, quantifying the variability or dispersion of outcomes from a series of trials with two possible results, like success and failure. It helps users gauge the spread of expected results given a specific probability and number of trials.
Table of Contents
How to use this Binomial Standard Deviation Calculator
- Enter Values:
- Number of Trials (n): In the input field labeled "(n) Number of Trials or Sample Size," enter the total number of trials or experiments you plan to perform.
- Probability of Success (p): In the next input field labeled "(p) Probability of Success or Population Proportion," enter the probability of a success in a single trial. This value should be between 0 and 1 (inclusive).
- Calculate: After entering the values, click on the Calculate button. When you click this button, the tool computes the standard deviation using the formula for a binomial distribution:
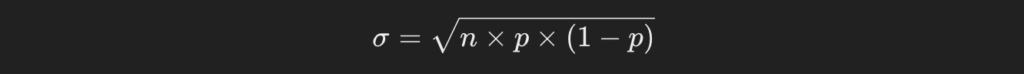
The result will be displayed under the buttons in the section labeled "Result," showing the standard deviation rounded to four decimal places.
- Reset: If you need to clear the input fields and start over, click on the Reset button. . Clicking this button will clear both input fields and any results displayed, allowing you to enter new values.
Usage Tips
- Ensure that your inputs are valid:
- Number of Trials (n) should be a positive integer.
- Probability of Success (p) should be a number from 0 to 1.
- Invalid entries will prompt an error message, asking you to enter valid values.
Where to use this Binomial Standard Deviation Calculator
The Binomial Standard Deviation Calculator can be used in various fields and scenarios to measure the variability of outcomes in binomial experiments where there are only two possible outcomes (like success and failure). Here are different applications or scenarios where this tool could be valuable:
- Quality Control: Determining the variability in defect rates of manufactured products.
- Clinical Trials: Assessing the spread in outcomes of new drugs or treatments, determining if results are consistent.
- Marketing Campaigns: Evaluating the success variability of different marketing strategies.
- Educational Testing: Measuring the consistency of student success rates in standardized tests or exams.
- Sports Performance: Analyzing the success rates of shots, goals, or hits in sports.
- Ecology Studies: Estimating the variability in survival rates of species under different environmental conditions.
- Financial Forecasting: Calculating the variability in loan defaults or credit risks.
- Political Polling: Understanding the variability in polling data, such as approval ratings or election outcomes.
- Inventory Management: Assessing the risk of stockouts in retail based on past sales data.
- Social Media Analysis: Evaluating the success rate of viral marketing campaigns or posts.
- Epidemiology: Analyzing the spread of disease and the consistency of infection rates.
- Insurance Underwriting: Estimating the variability of claims in different insurance categories.
- Engineering Reliability: Calculating the consistency of machinery or system failures.
- Customer Service: Analyzing the success rate of resolving customer issues or complaints.
- Game Development: Estimating the success rate of players completing levels or achieving goals in video games.
- Crime Analysis: Analyzing the success rate of solving cases based on different crime types or investigation methods.
- Agricultural Research: Estimating the variability in crop yields due to pest control methods or genetically modified seeds.
- Telecommunication Network Testing: Measuring the consistency of successful data packet transmissions over different network routes or conditions.
- Online Education Platforms: Evaluating the completion rates of online courses or tutorials to assess effectiveness and engagement.
- Renewable Energy Adoption: Analyzing the variability in community acceptance rates for new renewable energy projects such as solar or wind power installations.
Each of these scenarios can benefit from understanding the variability of binary outcomes, which helps in planning, risk management, and decision-making processes. The calculator assists in providing a mathematical basis for these assessments, making it easier to quantify and manage uncertainty in diverse fields.
Loved this tool? How about using our other Statistical Tools?